分类任务

混淆矩阵

Confusion Matrix		真实情况
		正	负
预测结果	正 Positive	真阳性 TP	伪阳性 FP
	负 Negative	伪阴性 FN	真阴性 TN

其中：

• 真阳性TP (True Positive)：将正类预测为正类数

• 伪阳性FP (False Positive)：将负类预测为正类数

• 伪阴性FN (False Negative)：将正类预测为负类数

• 真阴性TN (True Negative)：将负类预测为负类数

准确率 Accuracy

即：就是所有的预测正确（正类负类）的占总的比重。 公式：

\[Accuracy = \frac{tp+tn}{tp+tn+fp+fn}\]

精确率 Precision

查准率，即正确预测为正的占全部预测为正的比例。 公式：

\[Precision=\frac{tp}{tp+fp}\]

召回率 Recall

查全率，即正确预测为正的占全部实际为正的比例。公式：

\[Recall = \frac{tp}{tp+fn}\]

F1 score（H-mean）

F1值为算数平均数除以几何平均数，且越大越好，将Precision和Recall的上述公式带入会发现，当F1值小时，True Positive相对增加，而false相对减少，即Precision和Recall都相对增加，即F1对Precision和Recall都进行了加权。 公式：

\[\frac{2}{F_1}=\frac{1}{Precision}+\frac{1}{Recall}\]

转换之后：

\[F_1 =\frac{2*Precision*Recall}{Precision+Recall} =\frac{2TP}{2TP+FP+FN}\]

ROC曲线

ROC空间将伪阳性率（FPR）定义为 X 轴，真阳性率（TPR）定义为 Y 轴。即：

\[y = TPR = \frac{TP}{TP+FN} , x = FPR= \frac{FP}{FP+PN}\]

给定一个二元分类模型和它的阈值，就能从所有样本的（阳性／阴性）真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。从 (0, 0) 到 (1,1) 的对角线将ROC空间划分为左上／右下两个区域，在这条线的以上的点代表了一个好的分类结果（胜过随机分类），而在这条线以下的点代表了差的分类结果（劣于随机分类）。将同一模型每个阈值 的 (FPR, TPR) 座标都画在ROC空间里，就成为特定模型的ROC曲线。可以调整阈值的高低（将左上图的B垂直线往左或右移动），便会得出不同的伪阳性率与真阳性率，总之即得出不同的预测准确率。

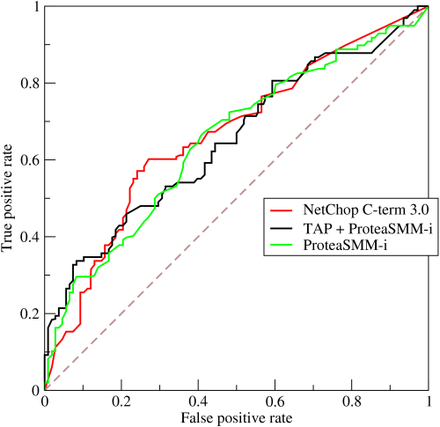
曲线下面积AUC

AUC即Area under the Curve of ROC (AUC ROC)，在比较不同的分类模型时，可以将每个模型的ROC曲线都画出来，比较曲线下面积做为模型优劣的指标。多数情况下，AUC值越大的分类器，正确率越高。

LogLoss

对于二分类任务，假如y是真实标签数据（0或1），p是预测概率（0.0～1.0），则LogLoss定义如下：

\[LogLoss = - \frac{1}{n} \sum_i { [ y_i\ * log(p_i) + ( 1-y_i)* log(1-p_i) ] }\]

LogLoss反映了样本的平均偏差，经常作为模型的损失函数来做优化。需要注意的是，则样本不均衡的情况下，LogLoss会偏向样本较多的一方。

—

其它：classification_report

sklearn提供的工具 classification_report 能够同时评估 precision、recall、F1等多个指标，如下：

• support:

例：support 为 58 代表y_test中class 0这一类的总数为58.

• micro avg:

微平均是分类正确的样本数与分类所有样本数的比值 (等于accuracy)，即： micro avg = (TP + FP) / (TP + TN + FP + FN) 例：示例中 micro avg = (0.91379 x 58 + 0.98230 x 113) / (58+113) = 0.95906

• macro avg:

宏平均是所有类的评估值的算术平均(设 β= 1) F1 macro avg = ( F1(class 0）+ F1(class 1）) / 2 = (0.93805 + 0.96943) / 2 = 0.95374